Jika nilai maksimum 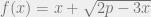 adalah
adalah  , maka nilai
, maka nilai  adalah …
adalah …
Jawab :
Nilai max/min terjadi pada saat
 nilai maksimum dari
nilai maksimum dari  adalah
adalah  , jadi
, jadi
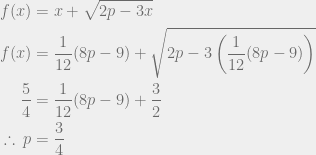
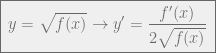
Jawab :
Nilai max/min terjadi pada saat
Jawaban : C
catatan :