Diketahui fungsi  dan
dan  dengan
dengan 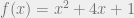 dan
dan 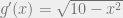 dengan
dengan 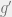 menyatakan turunan pertama fungsi
menyatakan turunan pertama fungsi  . Nilai turunan pertama
. Nilai turunan pertama  di
di 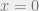 adalah …
adalah …
Jawab :
Misalkan , maka turunan dari
, maka turunan dari 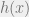 adalah …
adalah …
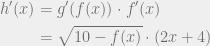 Sehingga turunan pertama
Sehingga turunan pertama  di
di 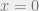 atau
atau  adalah
adalah

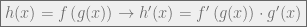
- 3
- 6
- 9
- 12
- 15
Jawab :
Misalkan
Jawaban : D
catatan :