Grafik fungsi  turun, jika …
turun, jika …
Jawab :
Fungsi akan turun jika turunan pertama,
akan turun jika turunan pertama, 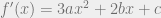 , bernilai negatif.
, bernilai negatif.
Syarat supaya selalu bernilai negatif adalah
selalu bernilai negatif adalah

Fungsi kuadrat akan selalu negatif, definit negatif, jika
akan selalu negatif, definit negatif, jika 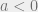 dan
dan 
Jawab :
Fungsi
Syarat supaya
Jawaban : E
catatan :Fungsi kuadrat